14 января

В продолжение разговора о проблемах цифровой передачи аналоговых сигналов, я публикую статью Сергея Подоляка, письмо которого на означенную тему было помещено в недавнем выпуске Компьютерры. Читатели dz online подвергли тезисы Сергея разнообразной критике, наиболее вразумительные :-) образцы которой я ему отослал. Сергей, будучи не в состоянии вступать в дискуссии на эту тему, тем не менее, предложил мне пару своих статей, которые более полно иллюстрируют его позицию в рамках обсуждаемой темы.

Отмечу, что по некоторым позициям Сергей и те, кто его критикует, как мне показалось, совпадают почти дословно, что, впрочем, не мешает им считать себя расположенными по разные стороны баррикад. :-)

Впрочем, смотрите сами. Я публикую сегодня первую из присланных статей.

Сергей Подоляк г.Винница, УКРАИНА 1997-1999г. аб/ящ 4225 Винница 286036 УКРАИНА (0432) 35-47-19 podoliak@usa.net

Все звуковые аналого-цифровые и цифро- аналоговые преобразователи, а также цифровые фильтры работают неправильно.

c Сергей Подоляк 1997. 26 Июля 1997г.

Уважаемые Господа!

В продолжение моих статей на тему борьбы с неприятностями в аудио технике, я бы хотел остановиться на одной тонкости аналого-цифрового и цифро-аналогового преобразования. Эта тонкость, будучи чисто математической, обычно упускается из вида при разработке цифровой звуковой аппаратуры - аналого-цифровых (АЦП) и цифро-аналоговых преобразователей (ЦАП) . Но сначала я скажу одну вещь, чтобы между нами всё сразу стало ясно:

Все звуковые аналого-цифровые и цифро- аналоговые преобразователи, а также цифровые фильтры работают неправильно!

Далее ваши вероятные вопросы выделены жирным шрифтом.

- Мы это и без вас подозревали давно. Ну и в чём там дело?

Дело в том, что, как известно, дискретизация аналоговых сигналов и их соответствующее восстановление из дискретного (точнее, амплитудно-импульсного) сигнала осуществляется (должно осуществляться) согласно теореме товарища В.А. Котельникова от 1933 года. Она гласит, что:

Периодическая (и удовлетворяющая условию Дирихле) функция времени (то есть процесс) с ограниченным спектром с максимальной частотой F может быть полностью восстановлена по дискретным отсчетам, взятым с периодом

T <= 1/2F.

(На самом деле здесь должен стоять знак строго "<", но об этом в другой раз).

- Ну и что, мы всё это читали и раньше.

Дело в том, что все известные автору современные аналого-цифровые и цифро-аналоговые преобразователи ограничивают спектр преобразуемого сигнала СВЕРХУ, но не СНИЗУ.

- Ну и что?

Теорема требует, чтобы восстанавливаемая <аналоговая> функция была периодической, то есть чтобы в ней не было спектральных компонент с частотой как угодно близких к 0 Hz. Таким образом, существует условие, чтобы спектр функции был ограничен СНИЗУ, причем это ограничение должно быть ничуть не хуже ограничения СВЕРХУ. То есть чем круче, тем лучше.

- Но это чисто математически? На практике ведь этого не надо? Ведь на практике частота 0 Hz почти никогда не преобразуется в АЦП и не восстанавливается в ЦАПе?

Нет, на самом деле данное условие имеет неожиданно естественное радиотехническое обоснование: для восстановления в ЦАП из отсчетов аналогового простого тонального сигнала, или сигнала с узким спектром, действительно достаточно пропустить амплитудно-импульсный сигнал через фильтр нижних частот, подавляющий только верхние частоты, обладающий небольшим временем задержки. При этом известно, что время задержки такого фильтра зависит от его крутизны затухания. Вообще говоря, для строгого выполнения условий теоремы необходимо, чтобы это время задержки было БЕСКОНЕЧНЫМ. То есть сигнал из идеального фильтра нижних частот вообще не выходит. Это несколько неожиданно, но математически якобы доказано. Теоретически, вы должны прочитать ВСЕ данные с вашего любимого компакт-диска в память CD-плейера, подождать пару часов, пока они там проинтерполируются аналоговым фильтром ЦАП-а, и только потом вы услышите музыку на вашей акустике. При применении в радиотехнике теоремы Котельникова обычно <подразумевают>, что бесконечное время здержки фильтра необходимо для эффективного подавления верхних частот амплитудно- импульсного сигнала. Однако при этом обычно упускают из вида, что это также необходимо для получения и накопления ВСЕХ ОТСЧЕТОВ, требуемых для восстановления сигналов с частотой близкой к нулю. В случае же, когда выходной сигнал ЦАП имеет широкий спектр (музыка), время задержки фильтра нижних частот должно быть больше разности периодов крайних спектральных составляющих широкополосного сигнала с прямоугольным спектром. В противном случае возникают нелинейные искажения сигнала. Для сигнала с непрямоугольным спектром имеется соответствующее интегральное выражение, которое мы опускаем для простоты изложения.

- Не совсем понятно...

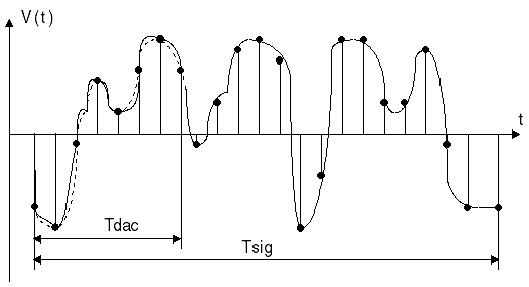
Возьмем типичный звуковой ЦАП. Время задержки сигнала в выходном аналоговом фильтре составляет порядка 5...10 милисекунд. Если требуется восстановить тональный (чистый) сигнал частотой 20Hz (период 50 милисекунд), то всё в порядке, существенных искажений и гармоник не возникает, хотя ЦАП (точнее, его выходной аналоговый фильтр нижних частот) начинает выдавать сигнал на выходе до получения всех необходимых для этого отсчетов. В этом случае фильтр ЦАП-а спасает то, что ширина спектра сигнала мала и необходимая задержка сигнала в фильтре также мала. Если же требуется восстановить сигнал с широким спектром, то фильтр ЦАП-а, из-за малого времени задержки, не обладая всей необходимой для этого информацией, выдает на выходе искаженный сигнал. Причем такие искажения имеют крайне нелинейный характер. На рис. 1 показана погрешность интерполяции широкополосного периодического сигнала по небольшому количеству точек, где:

Tsig - это период широкополосного сигнала;
Tdac - это время задержки фильтра цифро-аналогового преобразователя.

Между первыми 8 отсчётами пунктиром показан правильный сигнал, а жирной линией показан сигнал, который будет восстановлен по этим точкам фильтром ЦАП-а.

Для точного восстановления сигнала с периодом Tsig нужно иметь 23 точки, причём на вид аналогового сигнала МЕЖДУ первыми 8 точками, попадающими в период Tdac интерполяции ЦАП-а, влияют и последующие 15 точек. Они, однако, не попадают в период задержки (интерполяции) Tdac фильтра ЦАП-а и потому не могут повлиять на вид восстанавливаемого сигнала.

Рис. 1.

Это значит, что для точного восстановления сигнала с широким спектром выходной фильтр нижних частот должен обладать очень большим временем задержки.

- Насколько большим?

Это зависит от наименьшей и наивысшей частот спектра сигнала. Например, для сигнала с составляющими частотой 3 Hz и 10000 Hz время задержки должно быть не менее 300 милисекунд. Для создания такого фильтра требуются большие усилия конструктора. При работе такого фильтра неизбежно возникают дополнительные фазо-частотные искажения. Гораздо легче включить дополнительный фильтр верхних частот. Указанное здесь соотношение давно используется на практике в цифровых радиоприёмниках, где частота дискретизации и восстановления (интерполяции) равна удвоенной РАЗНОСТИ крайних частот спектра. Фильтр верхних частот нужен в силу неидеальности фильтра нижних частот, имеющего не бесконечное, а конечное время задержки, и потому имеющего нижнюю частотную границу восстанавливаемого широкополосного сигнала. Однако узкополосный (например, тональный измерительный) сигнал низкой частоты до единиц Герц может быть достаточно точно восстановлен и без фильтра верхних частот именно ввиду своей узкополосности.

- Но ведь нам не нужны 3 Hz.

Совершенно верно, нам с Вами нужны 20 Hz ...20 kHz. Однако частоты (интермодуляционных искажений, возникших при записи) ниже 20 Hz все равно содержатся в современных музыкальных записях и пропускаются современными ЦАПами. Здесь нужен фильтр ВЕРХНИХ частот. При этом фильтр верхних частот также необходим потому, что амплитудно-импульсный сигнал на выходе формирователя ступенчатого сигнала ЦАП-а может иметь очень широкий низкочастотный спектр вплоть до 0 Hz. В обычном же фильтре ЦАП-а происходит следующее. Сигнал на выходе фильтра нижних частот появляется через 5...10 мс после поступления первого отсчёта, то есть после принятия примерно 220...440 отсчётов. Это значит, что фильтр, недополучив до 2200 примерно 1800 точек интерполяции, считает, что у него есть вся информация для интерполяции широкополосного сигнала, и вносит нелинейные искажения в выходной сигнал, которые проявляются в виде низкочастотных <хвостов>, грохота, диссонансов. В силу всего сказанного, в математическом и радиотехническом смыслах теоремы отсчётов Котельникова для периодических сигналов частота 0 Hz представляет собой такую же бесконечность (минус бесконечность), как и собственно частота плюс бесконечность. Указанное условие ограничения спектра сигнала снизу устраняет так называемый <парадокс теоремы Агеева> [1]. Теорему Агеева можно интерпретировать так: если не ограничивать спектр дискретизируемой функции снизу, то может так случиться, что в некоторые произвольные моменты между двумя отсчетами функция должна будет совершать как угодно большое число осцилляций (например, миллион колебаний между двумя отсчетами, воспроизводимыми с 44100 Hz компакт-диска с обычной музыкальной программой). То есть если не ограничивать спектр снизу, то в техническом смысле такую функцию невозможно восстановить, даже если она <правильно> дискретизирована.

- Но в аналоговом или цифровом фильтре восстановление идёт непрерывно, с накоплением полученной информации, поэтому низкие частоты восстанавливаются хорошо...

Отдавая энергию на своём выходе, аналоговый фильтр теряет и ИНФОРМАЦИЮ о накопленных отсчётах, поэтому время задержки фильтра однозначно определяет количество дискретных выборок, по которым он ведёт интерполяцию. Для восстановления сигнала с широким спектром от 20 Hz до 20 kHz необходимо накопление 2000 (точнее, 2200 при частоте дискретизации 44100) точек отсчёта. Если бы это было не так, то можно бы было восстанавливать любой сигнал по двум отсчётам, и все цифровые фильтры вели бы расчёт по двум точкам. Данное условие подтверждается известным критерием восстановления Железнова [2,3]. Одно из условий критерия Железнова звучит так: количество N точек , необходимых для восстановления реального сигнала, равно: N = 4FT, где F - ширина эффективного спектра сигнала с конечной длительностью, T - длительность сигнала. Таким образом, для музыкального сигнала от 20 Hz до 20 kHz, имеющего длительность не менее его периода (1/20 Hz= 50 мсек), с шириной спектра 20 kHz, количество точек интерполяции должно быть не менее 4000! Однако критерий Железнова <слишком сильный>, поскольку предполагает неограниченность спектра функции (т.е. сигнала). Для музыкального сигнала с конпакт-диска <достаточно> не менее 2000 точек. Для накопления 2000 точек нужен фильтр с временем задержки 50 мс, Для сигнала с полосой от 10 Hz до 20 kHz требуется время 100 мс, для сигнала с полосой от 0.1 Hz - 10 сек (!) ... и т.д. Поэтому надо договориться о нижней частоте полосы преобразуемого спектра сигнала. Например, 20...20000 Hz.

- А с точки зрения теории информации...

И здесь имеется подтверждение указанной зависимости. Тональный синусоидальный (неизменяющийся) сигнал не несёт в себе никакой информации, для его восстановления необходимо также небольшое количество информации (накопленных отсчётов). Если точно известна его частота, то для восстановления требуется всего две выборки, независимо от его амплитуды. Изменяющийся же аналоговый сигнал, например, модулированный, имеющий широкий спектр, несёт в себе информацию, и для его восстановления необходимо большее количество информации, то есть большее количество отсчётов, накопленных в выходном аналоговом фильтре.

- А может быть, всё это не так...

Подтверждение есть и в живой природе. Все бегающие существа, включая Homo Sapiens, имеют нижний и верхний частотный порог слышимости, причём с весьма крутым спадом. По всей видимости, в животной природе слуха акустический сигнал тоже дискретизируется. У человека, вероятно, база расчёта - около 20000 точек - равна количеству волосков ушной улитки, - намного превышает теоретически требуемую. Ухо работает с большим запасом (большой скоростью) для дискретизации и последующей обработки человеческой речи с изменчивым спектром (то есть акустической колебательной системы с множеством переменных параметров).

- Что тут можно сделать?

Во-первых, включить в состав студийных АЦП фильтр верхних частот, отрезающий низкие частоты до 20Hz. Во-вторых, включить в состав компакт-диск плейера цифровой фильтр верхних частот с большим завалом низких частот до 20 Hz. Этот фильтр должен включаться до ЦАП. Такой фильтр легко может включаться в состав цифрового фильтра передискретизации. В-третьих, включить на выходе ЦАП аналоговый фильтр верхних частот, отрезающий низкие частоты (до 20 Hz). Или применять на выходе ЦАП полосовой фильтр 20 Hz... 20 kHz. Кроме этого, желательно включить в воспроизводящий тракт кассетных аудио приставок и студийных <аналоговых> магнитофонов фильтр верхних частот, отрезающий низкие частоты до 20 Hz а также фильтр нижних частот, отрезающий высокие частоты выше 20 kHz, поскольку сигнал, записанный на магнитной ленте с помощью высокочастотного подмагничивания, также представляет собой дискретные отсчёты аналогового сигнала (подробнее об этом см. журнал ©2, 1997, стр. 66). Кроме уже сказанного, производителей ЦАП-ов надо обязать указывать время задержки сигнала в выходном аналоговом фильтре.

- Значит будем улучшать аналоговые фильтры ЦАП-ов?

Подождите, ЦИФРОВЫЕ ФИЛЬТРЫ, в том числе передискретизационные, тоже нуждаются в переделке. Дело в том, что современные цифровые фильтры имеют базу, то есть количество последовательных точек (отсчётов), по которым идёт расчёт, около 50-80, иногда больше. Для сигналов с узким спектром (тональный измерительный сигнал) всё нормально, искажений нет. Но для широкополосных сигналов, например, от 20 Hz до 20 kHz, база цифровой фильтрации должна быть 2200 (последовательных точек, отсчётов). 2200=44100/20. Широкополосный аналоговый сигнал, содержащий множество компонент с частотами от 20 Hz до 20000 Hz можно восстановить ТОЛЬКО по 2200 точкам. Если база меньше указанной, а это сейчас общий случай, возникают нелинейные искажения произвольного порядка. Этим объясняется то, что не существует компакт-диска DDD, звучащего лучше, чем AAD, или хотя бы так же. В этом случае всё дело в том, что цифровые фильтры цифровых студийных пультов также имеют малую базу. Однако, по моему мнению, увеличение базы с 80 до 2200 связано с серьёзными вычислительными трудностями. Надо бороться дальше.

[1] Л.М. Финк <Сигналы, помехи, ошибки>. М. <Радио и связь> 1984.
[2] И.В. Кузьмин, В.А. Кедрус <Основы теории информации и кодировния>, Киев, 1977.
[3] Железнов Н.А. <Некоторые вопросы теории информационных электрических систем>. Л., изд- во ЛКВВИА, 1960.